Predicting relationships in bipartite graphs

In the case of bipartite graphs, the previous methods don't work well. Indeed, the algorithms consisting of closing the triangle are not appropriate.

Consider, for instance, the following graph:

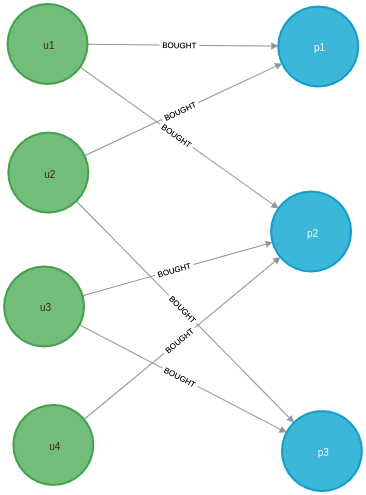
This graph can be created using the following Cypher:

CREATE (u1:User {name: "u1"})
CREATE (u2:User {name: "u2"})
CREATE (u3:User {name: "u3"})
CREATE (u4:User {name: "u4"})

CREATE (p1:Product {name: "p1"})
CREATE (p2:Product {name: "p2"})
CREATE (p3:Product {name: "p3"})

CREATE (u1)-[:BOUGHT]->(p1)
CREATE (u1)-[:BOUGHT]->(p2)
CREATE (u2)-[:BOUGHT]->(p1)
CREATE (u2)-[:BOUGHT]->(p3)
CREATE (u3)-[:BOUGHT]->(p2)
CREATE (u3)-[:BOUGHT]->(p3)
CREATE (u4)-[:BOUGHT]->(p2)

Users u1 and u2 both bought product p1. u1, u2, and p1 are therefore three corners of a possible triangle. However, closing this triangle by adding an edge between u1 and u2 is not possible since...