Let's look again at the following graph:
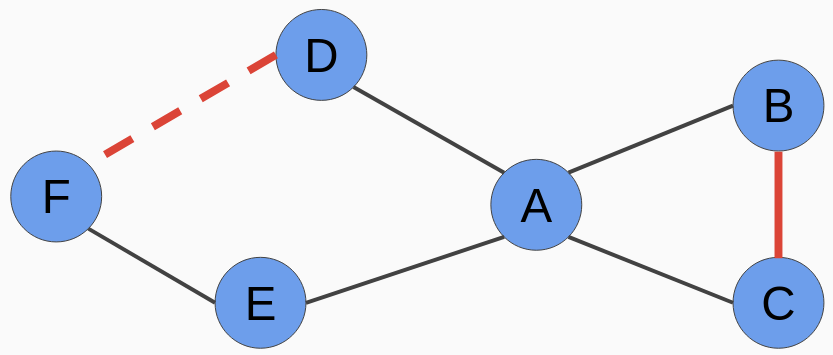
In the preceding graph, we can see that the relationship between B and C is more likely to be true than the one between D and F, because the shortest path between B and C is only 2 (unweighted graph), while the shortest path between D and F is 3.
So we can envisage a scoring function as follows:
score(u, v) = 1/d(u, v),
where d(u, v) is the shortest path between nodes u and v
In Chapter 4, The Graph Data Science Library and Path Finding, we studied the all pairs shortest path algorithm, which can be useful here if link prediction metrics based on distance are relevant for your problem. Remember that the algorithm can be run on a previously created, named projected graph, graph, using the following query:
CALL gds.alpha.allShortestPaths.stream("projected_graph", {})
YIELD sourceNodeId, targetNodeId, distance
WITH gds.util.asNode(sourceNodeId) as startNode,
gds.util.asNode(targetNodeId) as endNode,
...































































