The Adamic-Adar score is an improvement on the common neighbors approach. Adamic-Adar assumes that rare connections give more information than common ones. In the Adamic-Adar formula, each relationship with a neighbor is weighted by the inverse of the neighbor's degree according to the following formula:
score(u, v) = Σi 1/log|N(i)|, i ∈ N(u) ∩ N(v)
This idea is illustrated in the following diagram.
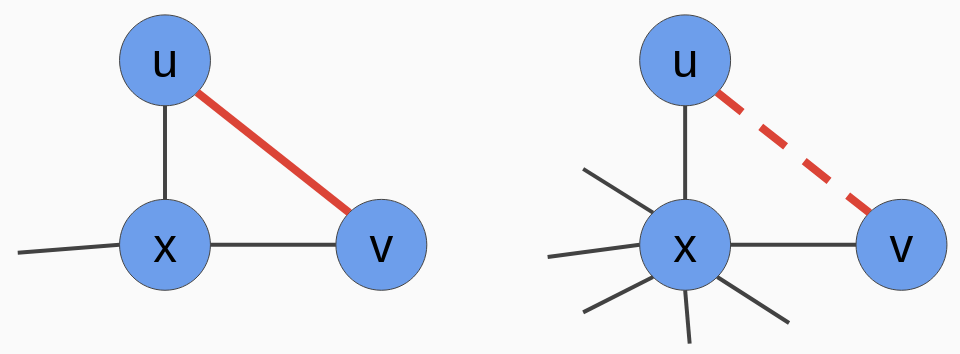
While nodes u and v are connected through x on both sides, since x has a lower degree on the left graph, its relationship to u and v is more important and the edge between u and v is more probable:
































































