A spanning tree is built from the original graph such that:
- The nodes in the spanning tree are the same as in the original graph.
- The spanning tree edges are chosen in the original graph such that all nodes in the spanning tree are connected, without creating loops.
The next figure illustrates some spanning trees for the graph we have studied in this chapter:
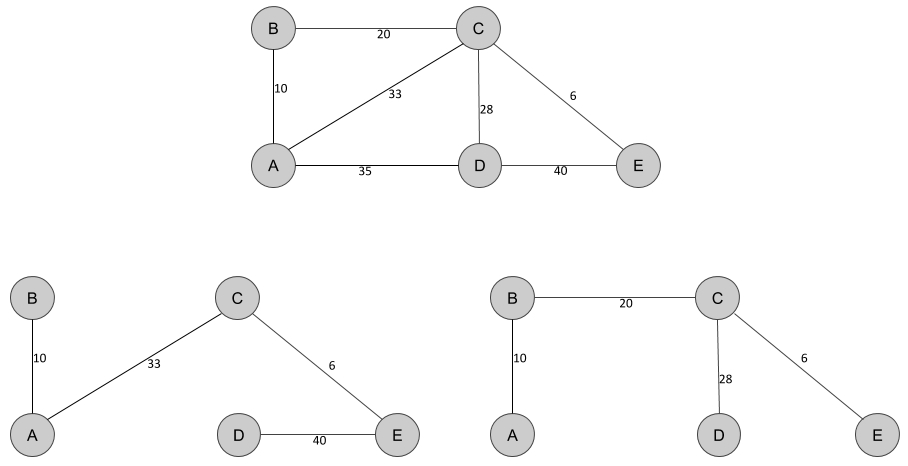
Among all possible spanning trees, the minimal spanning tree is the spanning tree with the lowest sum of weight for all edges. In the preceding diagram, the bottom-left spanning tree has a total sum of weights of 89 (10+33+6+40), while the bottom-right spanning tree has a total sum of weights of 64 (10+20+28+6). The bottom-right spanning tree is hence more likely to be the minimal spanning tree. To verify this, in the following section, we will discuss the algorithm implemented in the GDS plugin to find spanning trees, Prim's algorithm.
































































