Binary numbering system
Unlike the decimal numbering system that has base 10 and uses ten digits, the binary numbering system is the base 2 and uses two digits, that is, 0 and 1. As such, the binary numbering system has had a number of applications in technology, especially in the field of electronics.
Table C.1 represents the both decimal and binary numbering systems:
Decimal | Binary |
0 | 0000 |
1 | 0001 |
2 | 0010 |
3 | 0011 |
4 | 0100 |
5 | 0101 |
6 | 0110 |
7 | 0111 |
8 | 1000 |
9 | 1001 |
10 | 1010 |
11 | 1011 |
12 | 1100 |
13 | 1101 |
14 | 1110 |
15 | 1111 |
Decimal to binary conversion
For me, the simplest conversion method for decimal to binary conversion is by using the following table:

Table C.2. Decimal to binary conversion
Example: Conversion of decimal number 19610 to binary number ?2
To convert decimal number 196 to binary, in table C.2 from left to right, begin placing 0s and 1s until you reach decimal number 196. You will enter 1s for numbers that are part of the calculation, and 0s for the numbers that are not part of the calculation. In that way, you will get the numbers 128 + 64 + 4 = 196. Finally, the string made up of 0s and 1s represents the result of the decimal to binary conversion. That being said, 196 in decimal is equal to 11000100 in binary (see Table C.3).
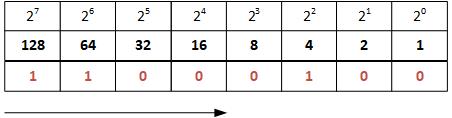
Table C.3. Converting decimal number 196 to binary number 11000100
Binary to decimal conversion
As it was the case with decimal to binary conversion, table C.2. will be used for converting numbers from binary to decimal. In this case, 0s and 1s are placed from right to left, as shown in Table C.4.
Example: Conversion of binary number 101011002to decimal number ?10
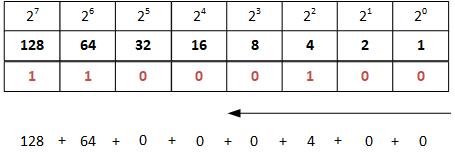
Table C.4. Converting the binary number 11000100 to decimal number 196
Like that, 11000100 in binary is equal to 196 in decimal.




































































