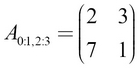Basic data structures

Scalar

A scalar is a single number unlike a matrix or a vector. For example, 1.3 is a scalar. A scalar can be mathematically denoted as follows: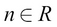

Here, R is the real number space.

Vectors

A vector is an array of numbers. Unlike a set, where there is no order to elements, a vector has a certain order to the elements. An example vector is [1.0, 2.0, 1.4, 2.3]. Mathematically, it can be denoted as follows:

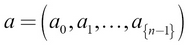
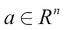
Alternatively, we can write this as:

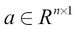
Here, R is the real number space and n is the number of elements in the vector.

Matrices

A matrix can be thought of as a two-dimensional arrangement of a collection of scalars. In other words, a matrix can be thought of as a vector of vectors. An example matrix would be as shown here:

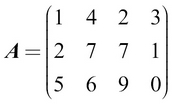
A more general matrix of size 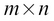can be mathematically defined like this:

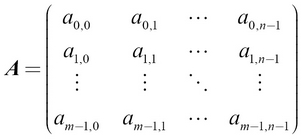
And:

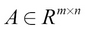
Here, m is the number of rows of the matrix, n is the number of columns in the matrix, and R is the real number space.

Indexing of a matrix

We will be using zero-indexed notation (that is, indexes start with 0).

To index a single element from a matrix at (i, j)^th position, we use the following notation:

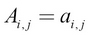
Referring to the previously defined matrix, we get the following:

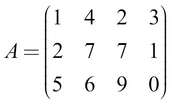
We index an element from A like this:

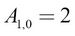
We denote a single row of any matrix A as shown here:

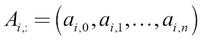
For our example matrix, we can denote the second row (indexed as 1) of the matrix as shown here:

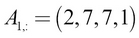
We denote the slice starting from the (i, k)^th index to the (j, l)^th index of any matrix A as shown here:

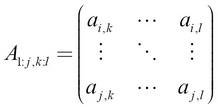
In our example matrix, we can denote the slice from first row third column to second row fourth column as shown here: