Logistic regression
Our first classification model is called logistic regression. I can already hear the questions you have in your head: what makes is logistic, why is it called regression if you claim that this is a classification algorithm? All in good time, my friend.
Logistic regression is a generalization of the linear regression model adapted to fit classification problems. In linear regression, we use a set of quantitative feature variables to predict a continuous response variable. In logistic regression, we use a set of quantitative feature variables to predict probabilities of class membership. These probabilities can then be mapped to class labels, thus predicting a class for each observation.
When performing linear regression, we use the following function to make our line of best fit:
y=
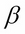 0 +
0 + 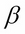 1x
1x
Here, y is our response variable (the thing we wish to predict), our Beta represents our model parameters and x represents our input variable (a single one in this case, but it can take...



























































