Confidence intervals

The central limit theorem gives us a systematic way to estimate population means, which is essential to the quality control of automated production in many sectors of the economy, from farming to pharmaceuticals.

For example, suppose a manufacturer has an automated machine that produces ball bearings that are supposed to be 0.82 cm in diameter. The quality control department (QCD) takes a random sample of 200 ball bearings and finds that sample mean to be 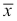= 0.824 cm. From long-term previous experience, they have determined that machine's standard deviation s σ = 0.042 cm. Since n = 200 is large enough, we can assume that z is nearly distributed as the standard normal distribution, where:

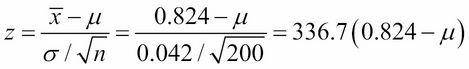
Suppose that the QCD has a policy of 95% confidence, which can be interpreted as meaning that it tolerates error only 5% of the time. So their objective is to find an interval (a, b) within which we can be 95% confident that the unknown population mean µ lies; that is, P(a ≤ µ ≤ b...