Rotations

Now, let's see the process that helps the red-black tree to balance (and therefore to maintain some of its color conditions): tree rotations.

Tree rotation is a mechanism that moves nodes of the tree to a different place in order to change the height of some of the nodes (and make it uniform among all the children). Let's see two different scenarios that we are going to use later in the insertion process: right rotation and left rotation.

Right rotation

We use a rotation to the right in the following scenario:

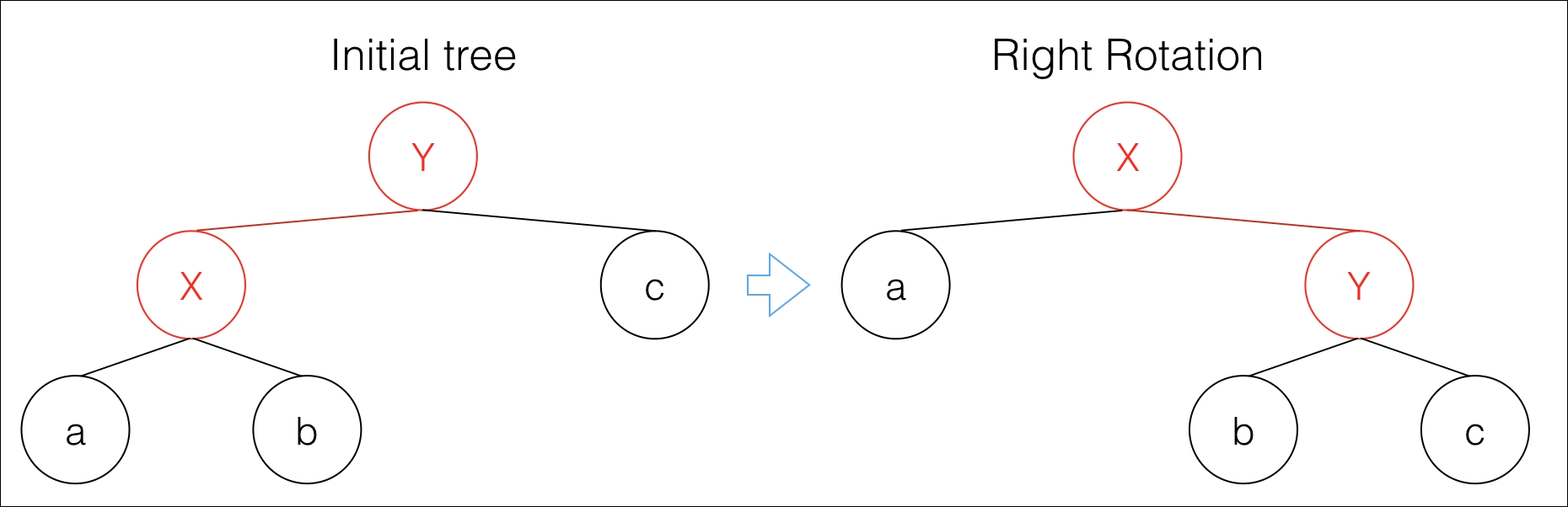
Right rotation in red-black trees

Here are the steps for right rotation:

1. Node X goes up to become the root of the new tree after the rotation (on the right side of the figure). Node Y, which was the parent of X, is now the right child (its value is greater, so it must be on the right subtree).

2. If node Y had a parent, we now assign that parent to node X.

3. The right child of node X is now the left child of its child node, Y.

Now, let's see how to implement this in Swift. Add a new...