Adjacency matrices

A matrix is a way of describing pairwise relationships. A matrix looks like a grid of numbers, as in the following example:

┌           ┐
│ 0    1 42 │
│ 0.5 -3  1 │
└           ┘

The preceding matrix contains six entries, organized in two rows and three columns. A matrix can have any number of rows or columns, but they are always rectangular. A matrix with two rows and three columns is described as a 2 x 3 matrix. If the entire matrix is called A, then the element at row i and column j is called A_i,j. So, in the preceding example, A_2,1 = 0.5.

One way to represent a graph as a matrix is to place the weight of each edge in one element of the matrix (or a zero if there is no edge). So, an edge from v₃, to v₁ with a weight of 37 would be represented by A_3,1 = 37, meaning the third row has a 37 in the first column. This representation is called an adjacency matrix.

With a little thought, it can be shown that adjacency matrices are always square. The number of rows is the number of columns is the number of vertices. Similarly, there is nothing saying that A_i,j has to be the same as A_j,i, so adjacency matrices can easily represent a directed graph. For an undirected graph, A_i,j always equals A_j,i, so the matrix is symmetric across one diagonal.

As an example, consider this network from Chapter 1, What is a Network?:

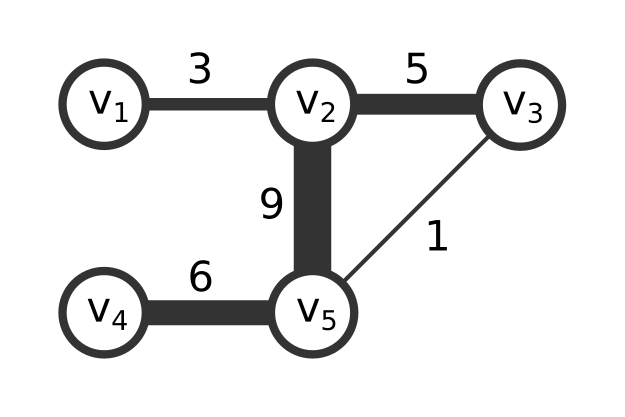
The corresponding adjacency matrix is as follows:

┌           ┐
│ 0 3 0 0 0 │
│ 3 0 5 0 9 │
│ 0 5 0 0 1 │
│ 0 0 0 0 6 │
│ 0 9 1 6 0 │
└           ┘

Matrices are more than just grids of numbers though! There are many mathematical operations that can be used to manipulate and combine matrices. For example, addition can be defined for two matrices by adding the elements at the same row and column. These operations can correspond to meaningful network processes. One such operation is the transpose, which exchanges A_i,j with A_j,i. The transpose of A is denoted as A^T and corresponds to reversing the direction of all edges.