Chapter 11. Red-Black Trees
In the previous chapter, we touched upon concepts such as amortization and balance in data structures. We need to balance the data structure so it does not degenerate. For example, in a Binary Search Tree (BST), if we insert elements that are already sorted, we get a tree, which is a linked list.
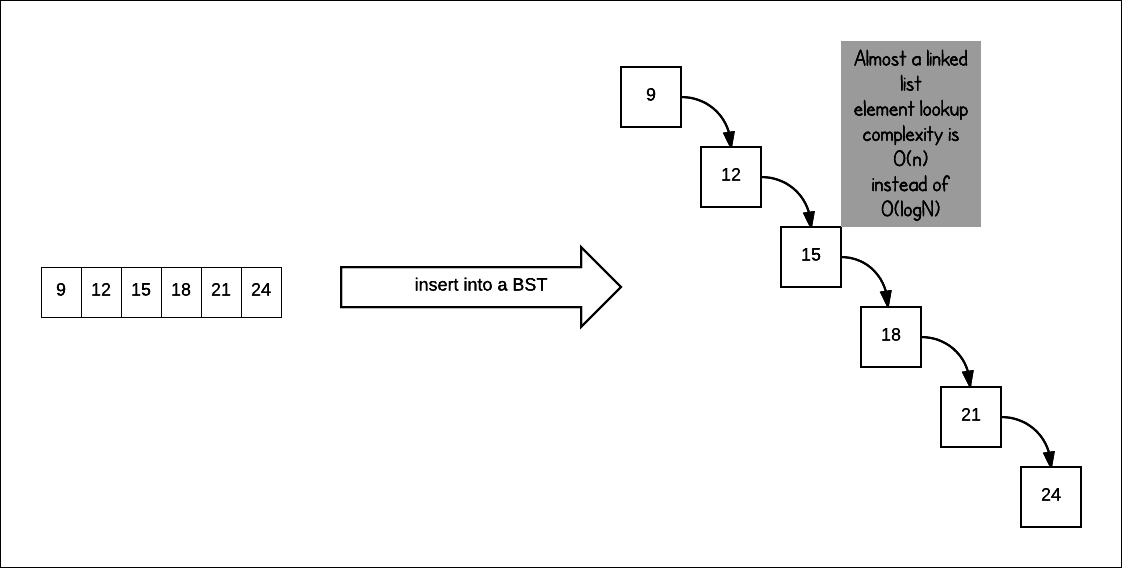
This is highly undesirable if we need a strong guarantee with respect to lookup complexity. Note that the insertion complexity is also O(n).
The solution is to balance the tree so things don't get out of hand. For example, if we could somehow ensure that the height of our tree is O(logn) for any data set, then we will have ensured O(logn) lookup and insertion/deletion.
Red-Black trees are basically BSTs. However, these trees are unique: every node sports a color, either red or black. This auxiliary information helps us keep the tree balanced, as we will soon see.




































































