Amortization
To better understand the concept of amortization, let's look at a dynamic array. This is an array that would grow if there is no space to add a new element. We could do this as follows:
Allocate a new array double the size of the current array.
Copy all the elements from the current array to the new array.
Make the new array the current array.
Here is a sample run of the algorithm depicted pictorially:
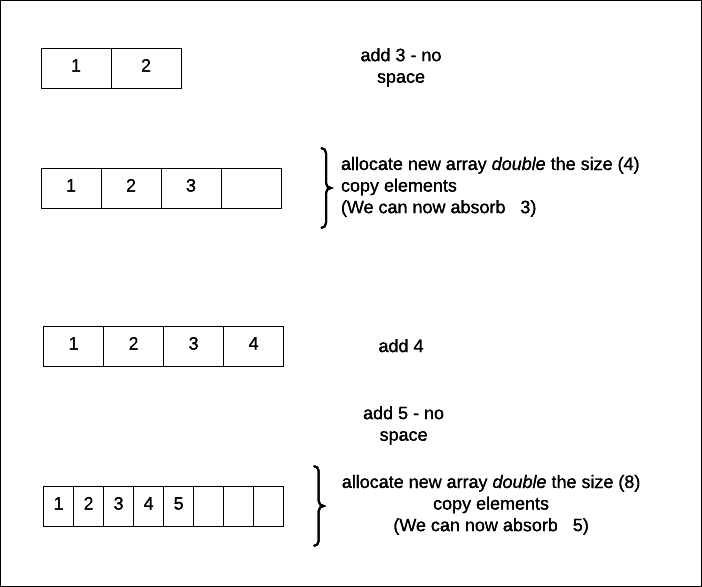
This allocation and copying obviously incur O(n) cost once in a while. If most of the elements incur a O(1) cost, we should be fine though.
If you continue to trace the growth of this array, you will soon realize that the allocate/copy operations occur less frequently as the number of elements grow.
Most of the insert operations would have O(1) complexity. In other words, an insertion would complete in amortized constant time.




































































