Ordering numbers was already a topic that we covered earlier in this book (Chapter 5, Robust Trees) while discussing trees: with heaps. A heap is a tree-like data structure with the highest (max-heap) or lowest number (min-heap) at the root that maintains order when inserting or removing elements. Hence, a sorting mechanism could be as simple as inserting everything into a heap and retrieving it again!
Since a (binary) heap has a known runtime complexity of O(log n), and the entire array has to be inserted, the estimated runtime complexity will be O(n log n), among the best sorting performances in sorting. The following diagram shows the binary heap in tree notation on the right, and the array implementation on the left:
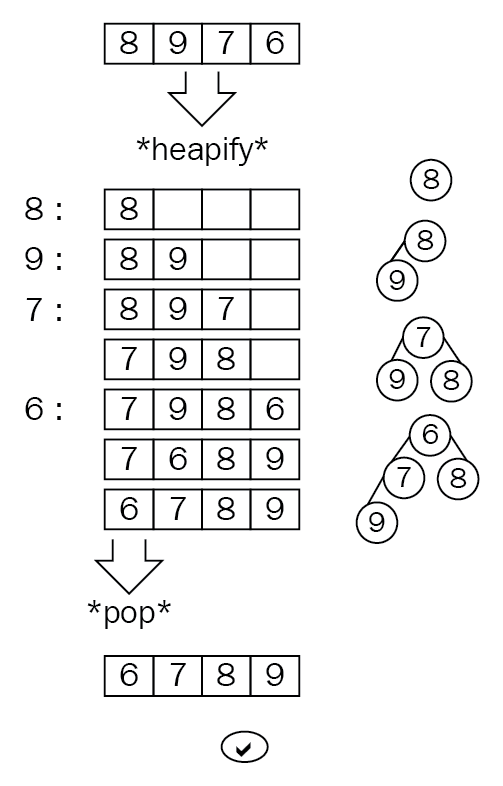
In the Rust standard library, there is a BinaryHeap structure available, which makes the implementation quick and easy:
pub fn heap_sort<T: PartialOrd + Clone + Ord>(collection: &[T]) -> Vec<T> {
let mut heap = BinaryHeap::new();
for...



































































