Going linearly over a collection one-by-one is only efficient if you are already close to a potential match, but it is very hard to determine—what does close to a match mean? In unordered collections, this is indeed impossible to know this since any item can follow. Consequently, what about sorting the collection first? As discussed in Chapter 9, Ordering Things, sorting at quasi-linear runtime complexity can be significantly faster than going over each item of a long collection past a certain size.
A jump search makes use of knowing about the range it jumps over, not unlike a skip list:
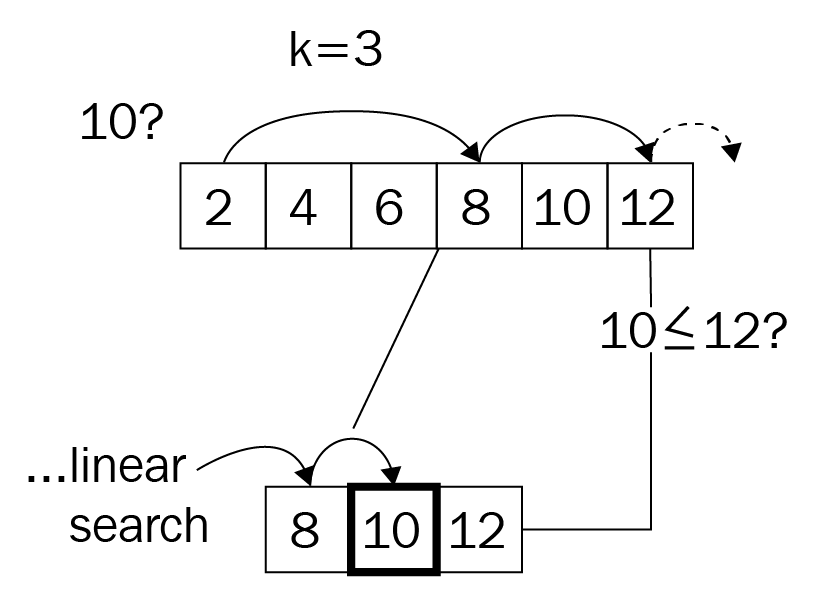
After sorting, a search can be significantly faster and a number of elements can be skipped in order to search in a linear fashion once the algorithm is close to a match. How many elements can be skipped at each jump? This is something to be tested, but first here is the code that does the work:
pub fn jump_search<T: Eq + PartialOrd + Clone>(
haystack: &[T],
needle...




































































