The elbow method is a well-known method for finding out the best number of clusters. In this method, we focus on the percentage of variance for the different numbers of clusters. The core concept of this method is to select the number of clusters that appending another cluster should not cause a huge change in the variance. We can plot a graph for the sum of squares within a cluster using the number of clusters to find the optimal value. The sum of squares is also known as the Within-Cluster Sum of Squares (WCSS) or inertia:
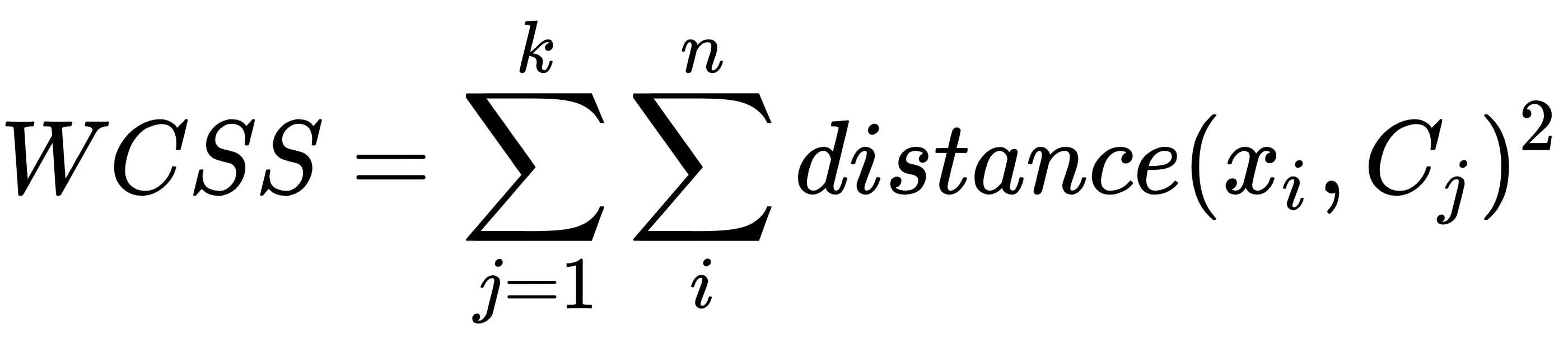
Here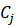
is the cluster centroid and 
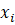is the data points in each cluster:
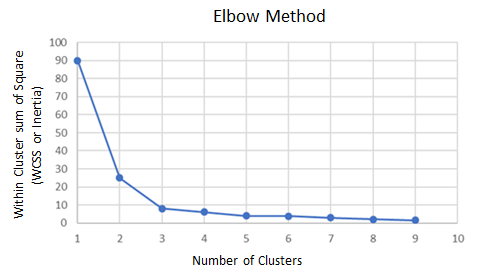
As you can see, at k = 3, the graph begins to flatten significantly, so we would choose 3 as the number of clusters.
Let's find the optimal number of clusters using the elbow method in Python:
# import pandas
import pandas as pd
# import matplotlib
import matplotlib.pyplot as plt
# import K-means
from sklearn.cluster import KMeans
# Create a DataFrame
data=pd.DataFrame...
