Calculating the eigenvalue and eigenvector of a matrix

One of the major advantages of eigenvalue calculation is its ability to reduce the dimensions of a dataset, which in turn reduces the computations required to solve a given set of variables.

The eigenvector of a given vector is the vector that satisfies the following condition:

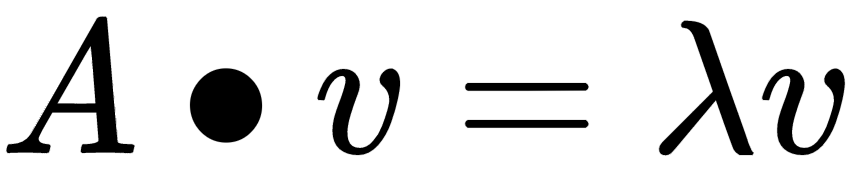
In the preceding equation, A is the matrix of our interest, v is the eigenvector, and λ is the eigenvalue of the given matrix.

How to do it…

In SciPy, we calculate the eigenvector and eigenvalue of a given matrix by using the eig function in scipy.linalg.

Using the following code, let us look at calculating the eigenvector and the corresponding eigenvalue of a given matrix:

1. Initialize a matrix:

a = np.array([[1, 2], [3, 4]])

2. Calculate the eigenvalue and eigenvector of the matrix:

la, v = linalg.eig(a)

3. The output of the preceding code is:

print(la)
[-0.37228132+0.j  5.37228132+0.j]
print(v)
[[-0.82456484 -0.41597356] [ 0.56576746 -0.90937671]]

Note that la is the eigenvalue...