Computing the norm and determinant

This subsection will introduce two important values in linear algebra, namely the norm and determinant. Briefly, the norm gives length of a vector. The most commonly used norm is the L²-norm, which is also known as the Euclidean norm. Formally, the L^p-norm of x is calculated as follows:

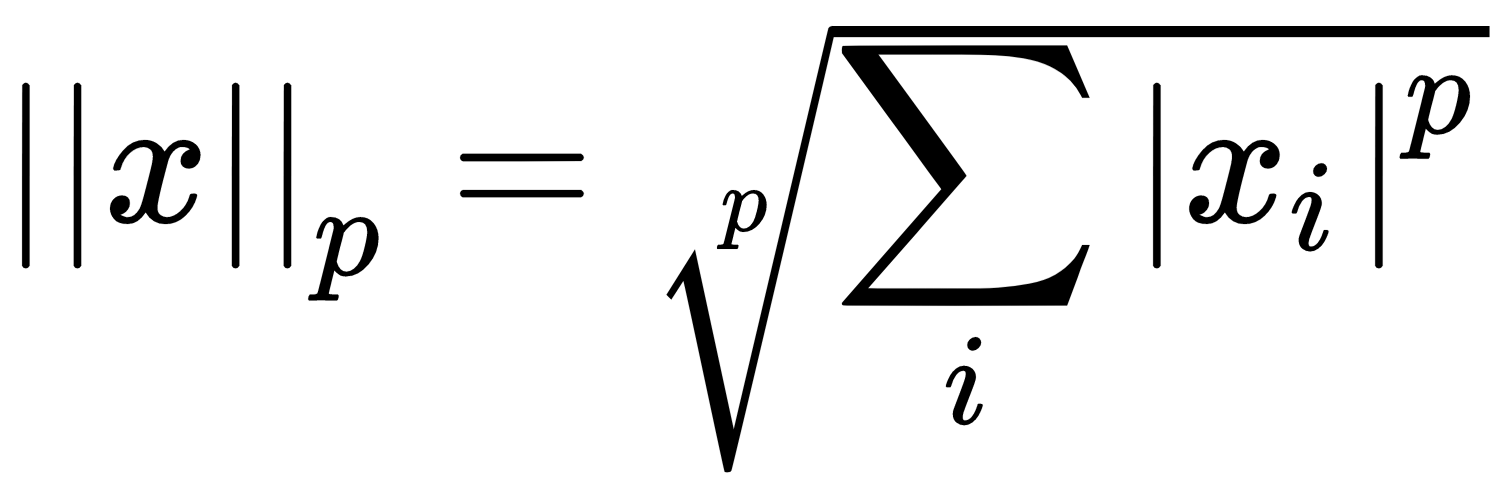
The L⁰-norm is actually the cardinality of a vector. You can calculate it by just counting the total number of non-zero elements. For example, the vector A =[2,5,9,0] contains three non-zero elements, therefore ||A||₀ = 3. The following code block shows the same norm calculation with numpy:

In [24]: import numpy as np 
         x = np.array([2,5,9,0]) 
         np.linalg.norm(x,ord=0)
Out[24]: 3.0 

In NumPy, you can calculate the norm of the vector with the use of the linalg.norm() method. The first parameter is the input array and the ord parameter is for order of the norm. The L¹-norm is also known as Taxicab norm or Manhattan norm. It calculates the length of the vectors...