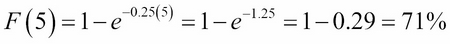The exponential distribution

Of all the probability distributions, the normal (Gaussian) distribution is maybe be the most important, because it applies to so many common phenomena. The second most important is probably the exponential distribution. Its density function is as follows:

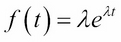
Here, λ is a positive constant whose reciprocal is the mean (µ = 1). This distribution models the time elapsed between randomly occurring events, such as radioactive particle emission or cars arriving at a toll booth. The corresponding cumulative distribution function (CDF) is as follows:

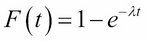
As an example, suppose that a university help desk gets 120 calls per eight-hour day, on average. That's 15 calls per hour, or one every four minutes. We can use the exponential distribution to model this phenomenon, with mean waiting time µ = 4. That makes the density parameter λ = 1/ µ = 0.25, so:

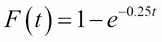
This means, for example, that the probability that a call comes in within the next five minutes would be: