Solving linear systems using matrices

A typical linear equation is expressed in the form of ax+by=c, where x and y are unknowns and a, b, and c are known values. Essentially, we are trying to find a relationship between a, b, and c.

There are multiple ways in which one is able to solve linear equations. In this recipe, we will be looking into the built-in function available in SciPy that helps us in solving a given linear system.

How it works…

The intuition behind solving for x and y is as follows:

([[a1 , b1 ],    x    ([x],    =    ([c1],  [a2 , b2 ]])          [y])            [c2])

For convenience, let's call the left-hand side matrix (a1, b1, a2, b2) the input matrix and the right-hand side matrix (c1, c2) the right-hand side vector.

The preceding matrix multiplication translates to:

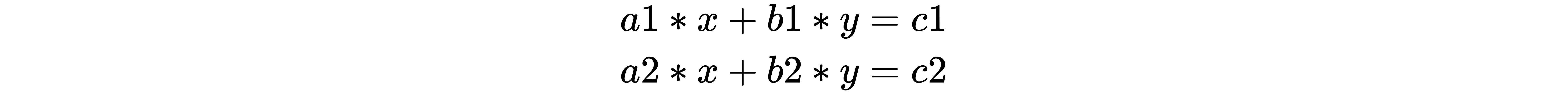
Given that there are two equations and two unknowns (x and y), we are in a position to solve for x and y. We should notice that, given that the matrix has two rows and columns with two unknowns, we can solve the...