The Bessel and Struve functions
In the next section, we will get into the details of the Bessel and Struve functions, and I am sure you are going to enjoy learning about them.
Getting ready...
Bessel functions are both of the canonical solutions to Bessel's homogeneous differential equation:
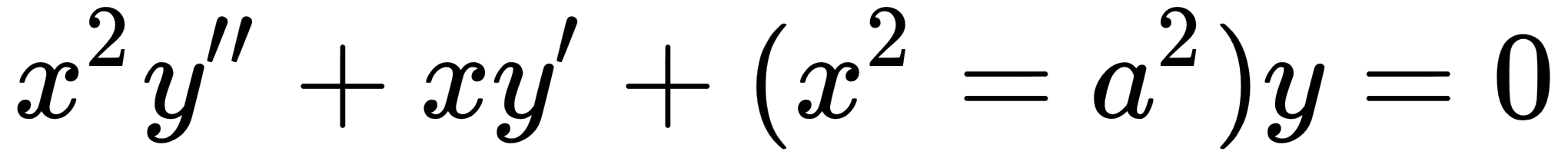
How to do it...
The Bessel and Struve functions are used as follows:
- These equations arise naturally in the solution of Laplace's equation in cylindrical coordinates
- The solutions of the non-homogeneous Bessel differential equation shown in the following diagram are called Struve functions
- We will follow the next equation and apply the proper function accordingly:
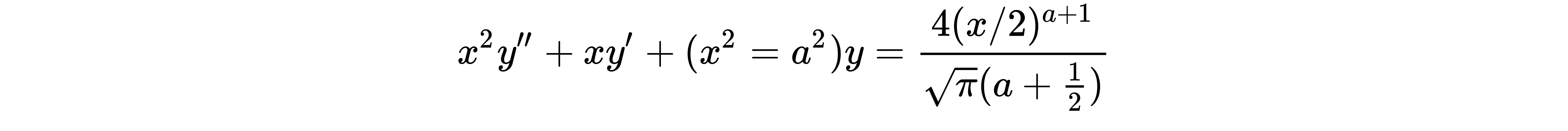
How it works...
These functions work as follows:
- In either case, the order of the equation is the complex number alpha which acts as a parameter. Depending on the canonical solution and the order, the Bessel and Struve functions are addressed (and computed) differently.
- For Bessel functions, we have algorithms to produce Bessel functions of the first...






































































