Definition of NPV and NPV rule

The Net Present Value (NPV) is defined by the following formula:

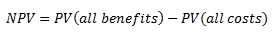
Here is an example. The initial investment is $100. The cash inflows in the next five years are $50, $60, $70, $100, and $20, starting from year one. If the discount rate is 11.2%, what is the project's NPV value? Since only six cash flows are involved, we could do the calculation manually:

>>> r=0.112
>>> -100+50/(1+r)+60/(1+r)**2+70/(1+r)**3+100/(1+r)**4+20/(1+r)**5
121.55722687966407
Using the scipy.npv() function, the estimation process could be simplified dramatically:
>>> import scipy as sp
>>> cashflows=[-100,50,60,70,100,20]
>>> sp.npv(0.112,cashflows)
121.55722687966407

Based on the preceding result, the NPV of this project is $121.56. A normal project is defined as follows: cash outflows first, then cash inflows. Anything else is an abnormal project. For a normal project, its NPV is negatively correlated with the discount rate; see the following...