RL as a Markov decision process
A Markov decision process (MDP) is a mathematical framework for modeling decisions. We can use it to describe the RL problem. We'll assume that we work with a full knowledge of the environment. An MDP provides a formal definition of the properties we defined in the previous section (and adds some new ones):
- is the finite set of all possible environment states, and st is the state at time t.

- is the set of all possible actions, and at is the action at time t.

- is the dynamics of the environment (also known as transition probabilities matrix). It defines the conditional probability of transitioning to a new state,s', given the existing state,s, and anaction,a (for all states and actions):

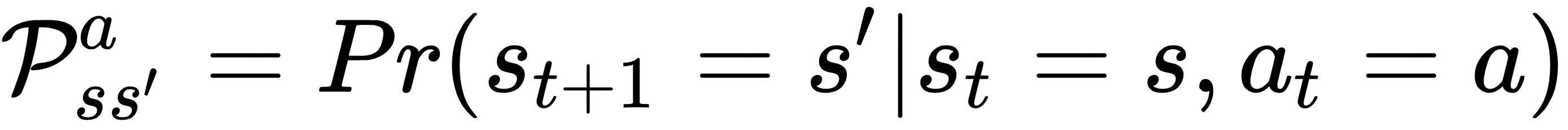
We have transition probabilities between the states, because MDP is stochastic (it includes randomness). These probabilities represent the model of the environment – that is, how it will likely change given its current state and an action,a. If the process were deterministic...







































































