Operations on a 4x4 matrix

We know how to find the minor, cofactor, and determinant of 2 X 2 and 3 X 3 matrices. In this section, we're going to implement those functions for a 4 X 4 matrix. We begin with the matrix of minors. The process for finding the minor of element i, j in a 4 X 4 matrix is the same as it was for a 3 X 3 matrix. We eliminate row i and column j of the matrix, the determinant of the resulting 3 X 3 matrix is the minor for element i, j.

Next, we find the cofactor. To find the cofactor we just follow the same formula we did for the 3 X 3 matrix:

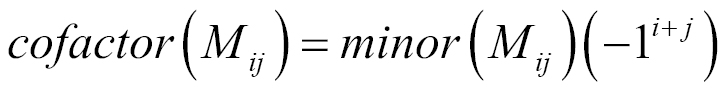
To get the cofactor of element i, j, we take the minor of that element and multiply it by 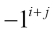. Finally, we have to find the determinant of the matrix. Again, we do this by following the same formula we used for the 3 X 3 matrix:

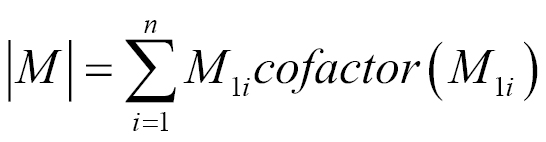
To find the determinant, we loop through any row of the matrix and sum up the result of multiplying each of the elements in the row by their respective cofactor. You only need to loop through one row, and which...