Determinant of a 3x3 matrix

We can find the determinant of any matrix through Laplace Expansion. We will be using this method to find the determinant of 3 X 3 and higher order matrices. We also used this method to find the determinant of 2 X 2 matrices; we just expanded the method by hand for that function to avoid looping:

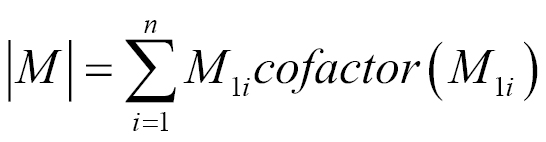
To follow the formula, we loop through the first row of the matrix and multiply each element with the respective element of the cofactor matrix. Then, we sum up the result of each multiplication. The resulting sum is the determinant of the matrix.

Using the first row is an arbitrary choice. You can do this equation on any row of the matrix and get the same result.

Getting ready

In order to implement this in code, first find the cofactor of the input matrix. Once we have a cofactor matrix, sum the result of looping through the first row and multiply each element by the same element in the cofactor matrix.

How to do it…

Follow these steps to implement a function which returns...