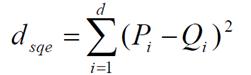In this article written by Sudipta Mukherjee, author of the book F# for Machine Learning, we learn about how information overload is almost a passé term; however, it is still valid. Information retrieval is a big arena and most of it is far from being solved. However, that being said, we have come a long way and the results produced by some of the state of the art information retrieval algorithms are really impressive. You may not know that you are using information retrieval but whenever you search for some documents on your PC or on the internet, you are actually using the produce of some information retrieval algorithm at the background. So as the metaphor goes, finding the needle (read information/insight) in a haystack (read your data archive on your PC or on the web) is the key to successful business.

• Distance based: Two documents are matched based on their proximity, calculated by several distance metric on the vector representation of the document
• Set based: Two documents are matched based on their proximity, calculated by several set based / fuzzy set based, metric based on the bag of words (BoW) model of the document

(For more resources related to this topic, see here.)

What are some interesting things that you can do?

You will learn how the same algorithm can find similar biscuits and identify author of digital documents from the words authors use. You will also learn how IR distance metrics can be used to group color images.

Information retrieval using tf-idf

Whenever you type some search term in your "Windows" search box, some documents appear matching your search term. There is a common, well-known, easy-to-implement algorithm that makes it possible to rank the documents based on the search term. Basically, the algorithm allows the developers to assign some kind of score to each document in the result set. That score can be seen as a score of confidence that the system has on how much the user would like that result.

The score that this algorithm attaches with each document is a product of two different scores. The first one is called term frequency (tf) and the other one is called inverse document frequency (idf). Their product is referred to as tf-idf or "term frequency inverse document frequency".

Tf is the number of times some term occurs in a given document. Idf is the ratio between the total number of documents scanned and the number of documents in which a given search term is found. However, this ration is not used as is. Log of this ration is used as idf, as shown next. The following is a term frequency and inverse term frequency example for the word "example":

This is the same as:

Idf is normally calculated with the following formula:

The following is the code that demonstrates how to find tf-idf score for the given search terms; in this case, "example". Sentences are fabricated to match up the desired number of count of the word "example" in document 2; in this case, "sentence2". Here  denotes the set of all the documents and  denotes a second document.

let sentence1 = "this is a a sample"

let sentence2 = "this is another another example example example"

let word = "example"

let numberOfDocs = 2.

let tf1 = sentence1.Split ' ' |> Array.filter ( fun t -> t = word) |> 
Array.length

let tf2 = sentence2.Split ' ' |> Array.filter ( fun t -> t = word) |> 
Array.length

let docs = [|sentence1;sentence2|]

let foundIn = docs |> Array.map ( fun t -> t.Split ' '

                                            |> Array.filter ( fun z 
-> z = word))

                                            |> Array.filter ( fun m 
-> m |> Array.length <> 0)

                                            |> Array.length

let idf =  Operators.log10 ( numberOfDocs / float foundIn)

let pr1 = float  tf1 * idf

let pr2 = float tf2 * idf

printfn "%f %f" pr1 pr2

This produces the following output:

0.0 ­ 0.903090

This means that the second document is more closely related with the word "example" than the first one. In this case, this is one of the extreme cases where the word doesn't appear at all in one document and appears three times in the other. However, with the same word occurring multiple times in both the documents, you will get different scores for each document. You can think of these scores as the confidence scores for association of the word and the document. More the score, more is the confidence that the document is bound to have something related to that word.

Measures of similarity

In the following section, you will create a framework for finding several distance measures. A distance between two probability distribution functions (pdf) is an important way to know how close two entities are. One way to generate the pdfs from histogram is to normalize the histogram.

Generating a PDF from a histogram

A histogram holds the number of times a value occurred. For example, a text can be represented as a histogram where the histogram values represent the number of times a word appears in the text. For gray images, it can be the number of times each gray scale appears in the image.

In the following section, you will build a few modules that hold several distance metrics. A distance metric is a measure of how similar two objects are. It can also be called a measure of proximity.

The following metrics use the notation of  and  to denote the ith value of either PDF. Let's say we have a histogram denoted by , and there are  elements in the histogram. Then a rough estimate of  is . The following function does this transformation from histogram to pdf:

let toPdf (histogram:int list)=

        histogram |> List.map (fun t -> float t / float 
histogram.Length )

There are a couple of important assumptions made. First, we assume that the number of bins is equal to the number of elements. So the histogram and the pdf will have the same number of elements. That's not exactly correct in mathematical sense. All the elements of a pdf should add up to 1. The following implementation of histToPdf guarantees that but it's not a good choice as it is not normalization. So resist the temptation to use this one.

let histToPdf (histogram:int list)=

        let sum = histogram |> List.sum

        histogram |> List.map (fun t -> float t / float sum)

Generating a histogram from a list of elements is simple. Following is the function that takes a list and returns the histogram. F# has the function already built in; it is called countBy.

let listToHist (l : int list)=

        l |> List.countBy (fun t -> t)

Next is an example of how using these two functions, a list of integer can be transformed into a pdf. The following method takes a list of integers and returns the probability distribution associated:

let listToPdf (aList : int list)=

        aList |> List.countBy (fun t -> t)

              |> List.map snd

              |> toPdf

Here is how you can use it:

let list = [1;1;1;2;3;4;5;1;2]

let pdf = list |> listToPdf

I have captured the following in the F# interactive and got the following histogram from the preceding list:

val it : (int * int) list = [(1, 4); (2, 2); (3, 1); (4, 1); (5, 1)]

If you just project the second element for this histogram and store it in an int list, then you can represent the histogram in a list. So for this example, the histogram can be represented as:

let hist = [4;2;1;1;1]

Distance metrics are classified among several families based on their structural similarity. The sections following show how to work on these metrics using F# and uses histograms as int list as input.

 and  denote the vectors that represent the entity being compared. For example, for the document retrieval system, these numbers might indicate the number of times a given word occurred in each of the documents that are being compared.  denotes the i element of the vector represented by  and  denotes the ith element of the vector represented by . Some literature call these vectors the profile vectors.

Minkowski family

As you can see, when two pdfs are almost the same then this family of distance metrics tends to be zero, and when they are further apart, they lead to positive infinity. So if the distance metric between two pdfs is close to zero then we can conclude that they are similar and if the distance is more, then we can conclude otherwise. All these formulae of these metrics are special cases of what's known as Minkowski distance.

• Euclidean distance

The following code implements Euclidean distance.

//Euclidean distance

let euclidean (p:int list)(q:int list) =

      List.zip p q |> List.sumBy (fun t -> float (fst t - snd 
t) ** 2.)

• City block distance

The following code implements City block distance.

let cityBlock (p:int list)(q:int list) =

    List.zip p q |> List.sumBy (fun t -> float (fst t  - snd 
t))

• Chebyshev distance

The following code implements Chebyshev distance.

let chebyshev(p:int list)(q:int list) =

        List.zip p q |> List.map( fun t -> abs (fst t - snd 
t)) |> List.max 

L1 family

This family of distances relies on normalization to keep the values within limit. All these metrics are of the form A/B where A is primarily a measure of proximity between the two pdfs P and Q. Most of the time A is calculated based on the absolute distance. For example, the numerator of the Sørensen distance is the City Block distance while the bottom is a normalization component that is obtained by adding each element of the two participating pdfs.

• Sørensen

The following code implements Sørensendistance.

let sorensen  (p:int list)(q:int list) =

        let zipped = List.zip (p |> toPdf ) (q|>toPdf)

        let numerator = zipped  |> List.sumBy (fun t -> float 
(fst t - snd t))

        let denominator = zipped |> List.sumBy (fun t -> float 
(fst t + snd t))

numerator / denominator

• Gower distance

The following code implements Gowerdistance. There could be division by zero if the collection q is empty.

let gower(p:int list)(q:int list)=

        //I love this. Free flowing fluid conversion

        //rather than cramping abs and fst t - snd t in a

        //single line

     let numerator = List.zip (p|>toPdf) (q |> toPdf)

                         |> List.map (fun t -> fst t - snd t)

                         |> List.map (fun z -> abs z)

                         |> List.map float

                         |> List.sum

                         |> float

     let denominator = float p.Length

     numerator / denominator

• Soergel

The following code implements Soergeldistance.

let soergel (p:int list)(q:int list) =

        let zipped = List.zip (p|>toPdf) (q |> toPdf)

        let numerator =  zipped |> List.sumBy(fun t -> abs( 
fst t - snd t))

        let denominator = zipped |> List.sumBy(fun t -> max 
(fst t ) (snd t))

        float numerator / float denominator

• kulczynski d

The following code implements Kulczynski ddistance.

let kulczynski_d (p:int list)(q:int list) =

        let zipped = List.zip (p|>toPdf) (q |> toPdf)

        let numerator =  zipped |> List.sumBy(fun t -> abs( 
fst t - snd t))

        let denominator = zipped |> List.sumBy(fun t -> min 
(fst t ) (snd t))

        float numerator / float denominator 

• kulczynski s

The following code implements Kulczynski sdistance.

let kulczynski_s (p:int list)(q:int list) =

/ kulczynski_d p q

• Canberra distance

The following code implements Canberradistance.

let canberra (p:int list)(q:int list) =

    let zipped = List.zip (p|>toPdf) (q |> toPdf)

    let numerator =  zipped |> List.sumBy(fun t -> abs( fst t 
- snd t))

    let denominator = zipped |> List.sumBy(fun t -> fst t + 
snd t)

    float numerator / float denominator

Intersection family

This family of distances tries to find the overlap between two participating pdfs.

• Intersection

The following code implements Intersectiondistance.

let intersection(p:int list ) (q: int list) =

        List.zip (p|>toPdf) (q |> toPdf)

•             |> List.map (fun t -> min (fst t) (snd t)) |>
  List.sum
  Wave Hedges

The following code implements Wave Hedgesdistance.

let waveHedges (p:int list)(q:int list)=

        List.zip (p|>toPdf) (q |> toPdf)

            |> List.sumBy ( fun t -> 1.0 - float( min (fst t) 
(snd t))

                                     / float (max (fst t) (snd 
t)))

• Czekanowski distance

The following code implements Czekanowski distance.

let czekanowski(p:int list)(q:int list) =

        let zipped  = List.zip (p|>toPdf) (q |> toPdf)

        let numerator = 2. * float (zipped |> List.sumBy (fun 
t -> min (fst t) (snd t)))

        let denominator =  zipped |> List.sumBy (fun t -> fst 
t + snd t)

        numerator / float denominator

• Motyka

The following code implements Motyka distance.

 let motyka(p:int list)(q:int list)=

       let zipped = List.zip (p|>toPdf) (q |> toPdf)

       let numerator = zipped |> List.sumBy (fun t -> min (fst 
t) (snd t))

       let denominator = zipped |> List.sumBy (fun t -> fst t 
+ snd t)

       float numerator / float denominator

• Ruzicka

The following code implements Ruzicka distance.

let ruzicka (p:int list) (q:int list) =

        let zipped = List.zip (p|>toPdf) (q |> toPdf)

        let numerator = zipped |> List.sumBy (fun t -> min 
(fst t) (snd t))

        let denominator = zipped |> List.sumBy (fun t -> max 
(fst t) (snd t))

        float numerator / float denominator

Inner Product family

Distances belonging to this family are calculated by some product of pairwise elements from both the participating pdfs. Then this product is normalized with a value also calculated from the pairwise elements.

• Innerproduct

The following code implements Inner-productdistance.

let innerProduct(p:int list)(q:int list)=

        List.zip (p|>toPdf) (q |> toPdf)

            |> List.sumBy (fun t -> fst t * snd t)

• Harmonic mean

The following code implements Harmonicdistance.

let harmonicMean(p:int list)(q:int list)=

       2. * (List.zip (p|>toPdf) (q |> toPdf)

          |> List.sumBy (fun t -> ( fst t * snd t )/(fst t + 
snd t)))

• Cosine similarity

The following code implements Cosine Similarity distance measure.

let cosineSimilarity(p:int list)(q:int list)=

    let zipped = List.zip p q

    let prod  (x,y) = float x *  float y

    let numerator = zipped |> List.sumBy prod

    let denominator  =  sqrt ( p|> List.map sqr |> List.sum |> 
float) *

                        sqrt ( q|> List.map sqr |> List.sum |> 
float)

    numerator / denominator

• Kumar Hassebrook

The following code implements Kumar Hassebrook distance measure.

  let kumarHassebrook (p:int list) (q:int list) =

        let sqr x = x * x

        let zipped = List.zip (p|>toPdf) (q |> toPdf)

        let numerator = zipped |> List.sumBy prod

        let denominator =  (p |> List.sumBy sqr) +

                           (q |> List.sumBy sqr) - numerator

 

        numerator / denominator

• Dice coefficient

The following code implements Dice coefficient.

  let dicePoint(p:int list)(q:int list)=    

        let zipped = List.zip (p|>toPdf) (q |> toPdf)

        let numerator = zipped |> List.sumBy (fun t -> fst t * 
snd t)

        let denominator  =  (p |> List.sumBy sqr)  +

                            (q |> List.sumBy sqr)

 

        float numerator / float denominator

Fidelity family or squared-chord family

This family of distances uses square root as an instrument to keep the distance within limit. Sometimes other functions, such as log, are also used.

• Fidelity

The following code implements FidelityDistance measure.

  let fidelity(p:int list)(q:int list)=      

        List.zip (p|>toPdf) (q |> toPdf)|> List.map  prod

                                        |> List.map sqrt

                                        |> List.sum 

• Bhattacharya

The following code implements Bhattacharya distance measure.

let bhattacharya(p:int list)(q:int list)=

        -log (fidelity p q)

• Hellinger

The following code implements Hellingerdistance measure.

let hellinger(p:int list)(q:int list)=     

       let product = List.zip (p|>toPdf) (q |> toPdf)

                         |> List.map prod |> List.sumBy sqrt

       let right = 1. -  product

       2. * right |> abs//taking this off will result in NaN

                  |> float

                  |> sqrt

• Matusita

The following code implements Matusita distance measure.

let matusita(p:int list)(q:int list)=

        let value =2. - 2. *( List.zip (p|>toPdf) (q |> toPdf)

                            |> List.map prod

                            |> List.sumBy sqrt)

        value |> abs |> sqrt

• Squared Chord

The following code implements Squared Chord distance measure.

let squarredChord(p:int list)(q:int list)=

        List.zip (p|>toPdf) (q |> toPdf)

            |> List.sumBy (fun t -> sqrt (fst t ) - sqrt (snd 
t))

Squared L2 family

This is almost the same as the L1 family, just that it got rid of the expensive square root operation and relies on the squares instead. However, that should not be an issue. Sometimes the squares can be quite large so a normalization scheme is provided by dividing the result of the squared sum with another square sum, as done in "Divergence".

• Squared Euclidean

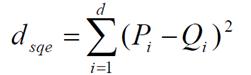
The following code implements Squared Euclidean distance measure. For most purpose this can be used instead of Euclidean distance as it is computationally cheap and performs as well.

let squaredEuclidean (p:int list)(q:int list)=

       List.zip (p|>toPdf) (q |> toPdf)

           |> List.sumBy (fun t-> float (fst t - snd t) ** 
2.0)

• Squared Chi

The following code implements Squared Chi distance measure.

let squaredChi(p:int list)(q:int list)=

        List.zip (p|>toPdf) (q |> toPdf)

           |> List.sumBy (fun t -> (fst t - snd t ) ** 2.0 / 
(fst t + snd t))

• Pearson's Chi

The following code implements Pearson’s Chidistance measure.

let pearsonsChi(p:int list)(q:int list)=

        List.zip (p|>toPdf) (q |> toPdf)

           |> List.sumBy (fun t -> (fst t - snd t ) ** 2.0 / 
snd t)

• Neyman's Chi

The following code implements Neyman’s Chi distance measure.

let neymanChi(p:int list)(q:int list)=

        List.zip (p|>toPdf) (q |> toPdf)

           |> List.sumBy (fun t -> (fst t - snd t ) ** 2.0 / 
fst t)

• Probabilistic Symmetric Chi

The following code implements Probabilistic Symmetric Chidistance measure.

let probabilisticSymmetricChi(p:int list)(q:int list)=

       2.0 * squaredChi p q

• Divergence

The following code implements Divergence measure. This metric is useful when the elements of the collections have elements in different order of magnitude. This normalization will make the distance properly adjusted for several kinds of usages.

let divergence(p:int list)(q:int list)=

        List.zip (p|>toPdf) (q |> toPdf)

            |> List.sumBy (fun t -> (fst t - snd t) ** 2. / 
(fst t + snd t) ** 2.)

• Clark

The following code implements Clark’s distance measure.

let clark(p:int list)(q:int list)=

     

        sqrt( List.zip (p|>toPdf) (q |> toPdf)

        |> List.map (fun t ->  float( abs( fst t - snd t))

                               / (float (fst t + snd t)))

 

        |> List.sumBy (fun t -> t * t))

• Additive Symmetric Chi

The following code implements Additive Symmetric Chi distance measure.

let additiveSymmetricChi(p:int list)(q:int list)=

        List.zip (p|>toPdf) (q |> toPdf)

            |> List.sumBy (fun t -> (fst t - snd t ) ** 2. * 
(fst t + snd t)/ (fst t * snd t)) 

Summary

Congratulations!! you learnt how different similarity measures work and when to use which one, to find the closest match. Edmund Burke said that, "It's the nature of every greatness not to be exact", and I can't agree more. Most of the time the users aren't really sure what they are looking for. So providing a binary answer of yes or no, or found or not found is not that useful. Striking the middle ground by attaching a confidence score to each result is the key. The techniques that you learnt will prove to be useful when we deal with recommender system and anomaly detection, because both these fields rely heavily on the IR techniques.

Resources for Article:

Further resources on this subject:

• Learning Option Pricing [article]
• Working with Windows Phone Controls [article]
• Simplifying Parallelism Complexity in C# [article]