The binary heap data structure
The binary heap is a special binary tree with the following two properties:
- It is a complete binary tree, meaning all levels of the tree have both left and right children (with the exception of the last-level leaves), and the last level has all children as left as possible. This is called as shape property.
- A binary heap is either a min heap or a max heap. The min heap allows you to quickly extract the minimum value of the tree, and the max heap allows you to quickly extract the maximum value of the tree. All nodes are either greater than or equal to (max heap), or less than or equal to (min heap), each of its child nodes. This is called heap property.
The following diagram contains some examples of invalid and valid heaps:
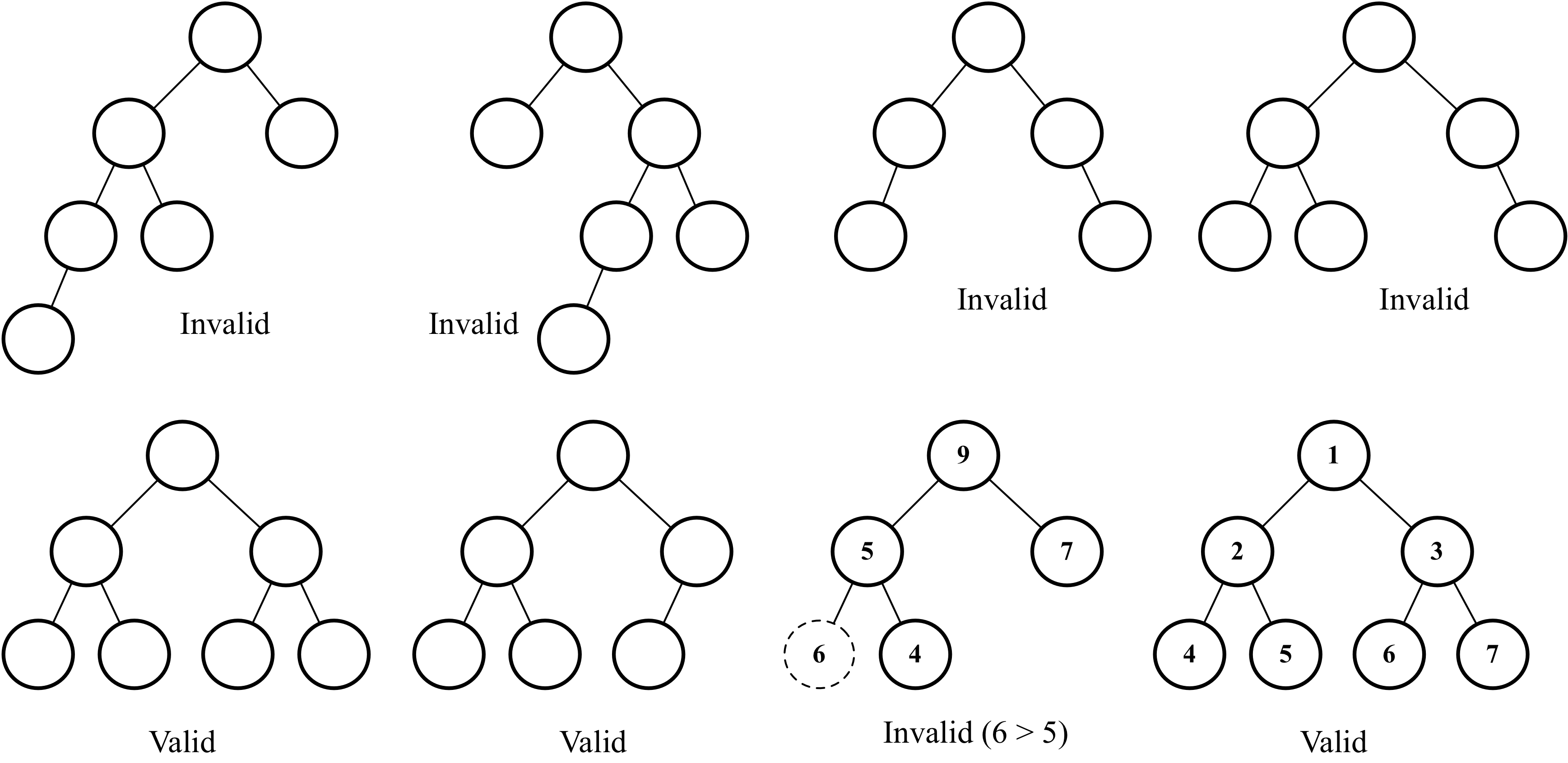
Although the binary heap is a binary tree, it is not necessarily a binary search tree (BST). In the binary heap, every child node needs to be greater than or equal to its parent node (min heap) or less than or equal to its parent node (max...




































































