Distribution Plots
Distribution plots give a deep insight into how your data is distributed. For a single variable, a histogram is effective. For multiple variables, you can either use a box plot or a violin plot. The violin plot visualizes the densities of your variables, whereas the box plot just visualizes the median, the interquartile range, and the range for each variable.
Histogram
A histogram visualizes the distribution of a single numerical variable. Each bar represents the frequency for a certain interval. Histograms help get an estimate of statistical measures. You see where values are concentrated, and you can easily detect outliers. You can either plot a histogram with absolute frequency values or, alternatively, normalize your histogram. If you want to compare distributions of multiple variables, you can use different colors for the bars.
Use
Get insights into the underlying distribution for a dataset.
Example
The following diagram shows the distribution of the Intelligence Quotient (IQ) for a test group. The dashed lines represent the standard deviation each side of the mean (the solid line):
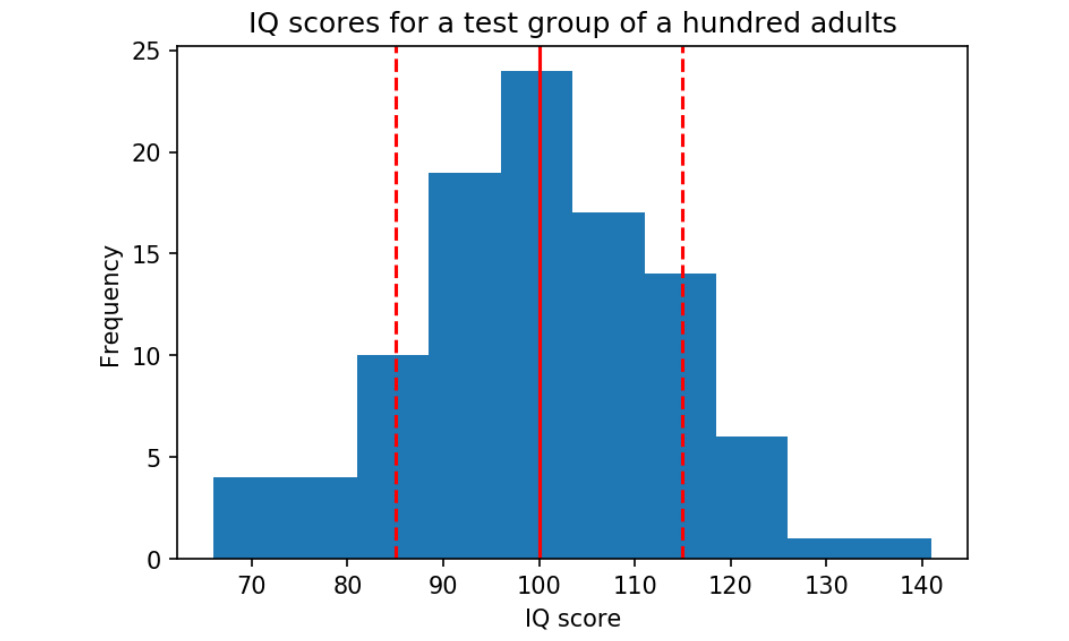
Figure 2.30: Distribution of IQ for a test group of a hundred adults
Design Practice
- Try different numbers of bins (data intervals), since the shape of the histogram can vary significantly.
Density Plot
A density plot shows the distribution of a numerical variable. It is a variation of a histogram that uses kernel smoothing, allowing for smoother distributions. One advantage these have over histograms is that density plots are better at determining the distribution shape since the distribution shape for histograms heavily depends on the number of bins (data intervals).
Use
To compare the distribution of several variables by plotting the density on the same axis and using different colors.
Example
The following diagram shows a basic density plot:
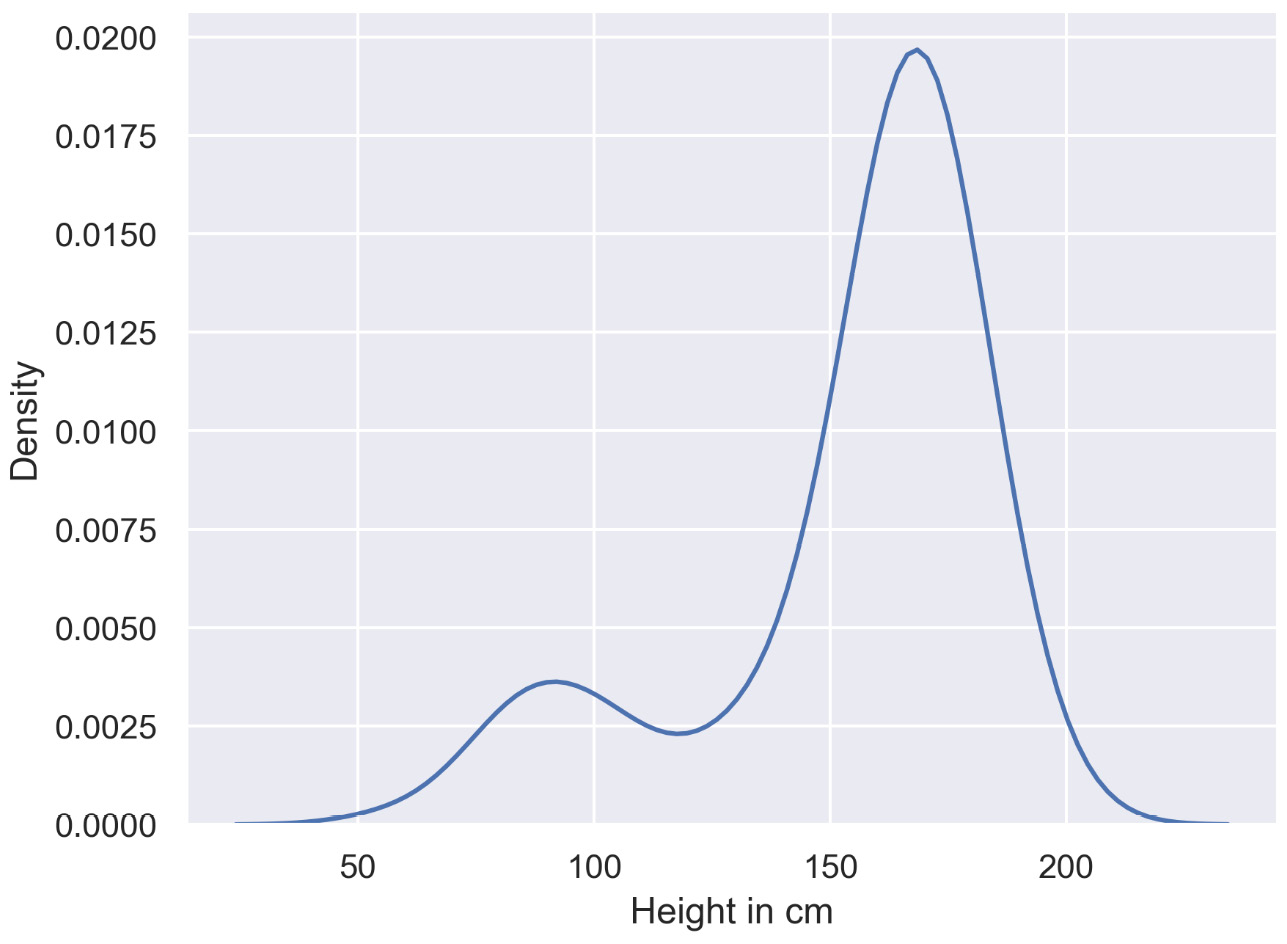
Figure 2.31: Density plot
The following diagram shows a basic multi-density plot:
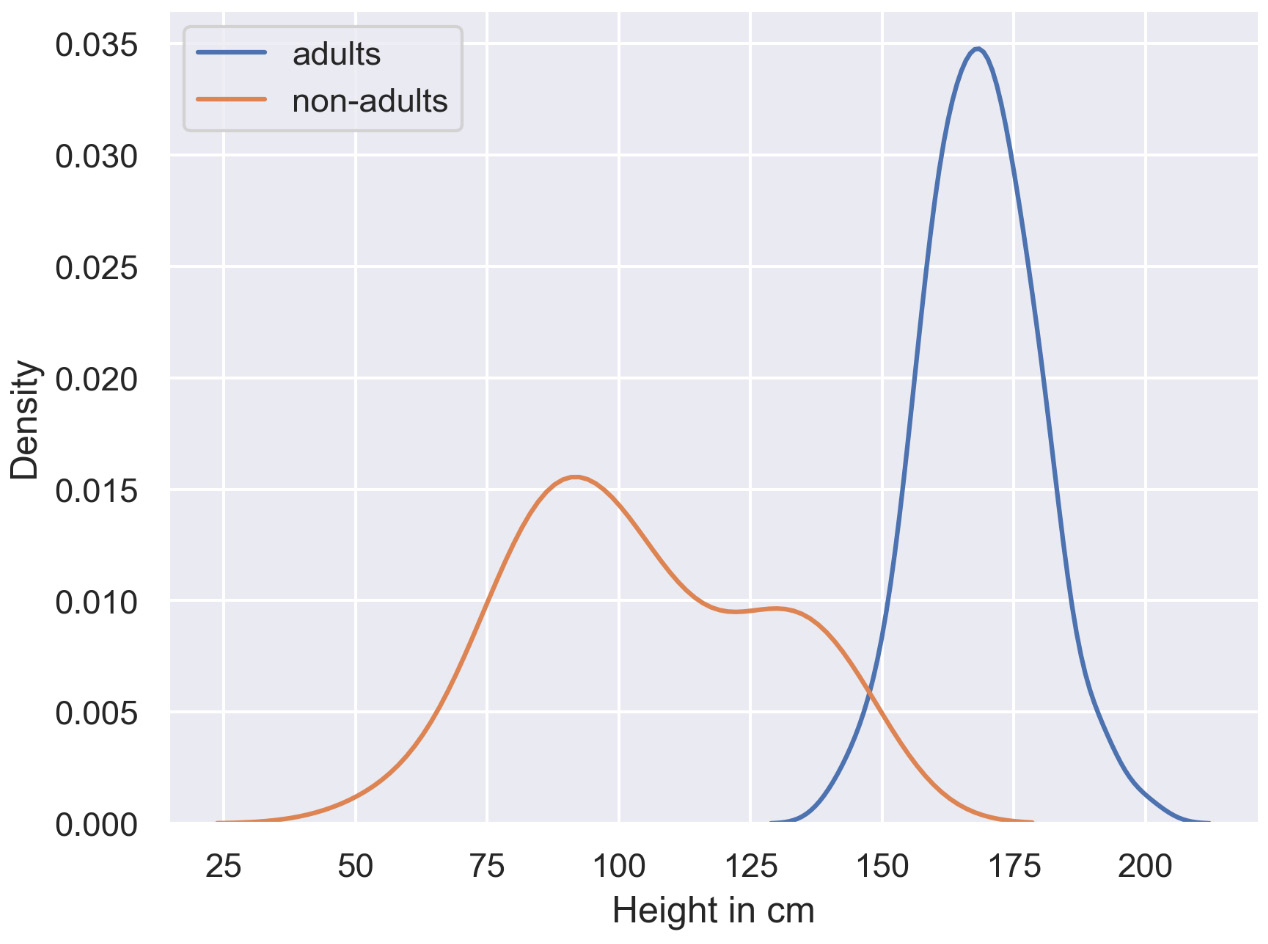
Figure 2.32: Multi-density plot
Design Practice
- Use contrasting colors to plot the density of multiple variables.
Box Plot
The box plot shows multiple statistical measurements. The box extends from the lower to the upper quartile values of the data, thus allowing us to visualize the interquartile range (IQR). The horizontal line within the box denotes the median. The parallel extending lines from the boxes are called whiskers; they indicate the variability outside the lower and upper quartiles. There is also an option to show data outliers, usually as circles or diamonds, past the end of the whiskers.
Use
Compare statistical measures for multiple variables or groups.
Examples
The following diagram shows a basic box plot that shows the height of a group of people:
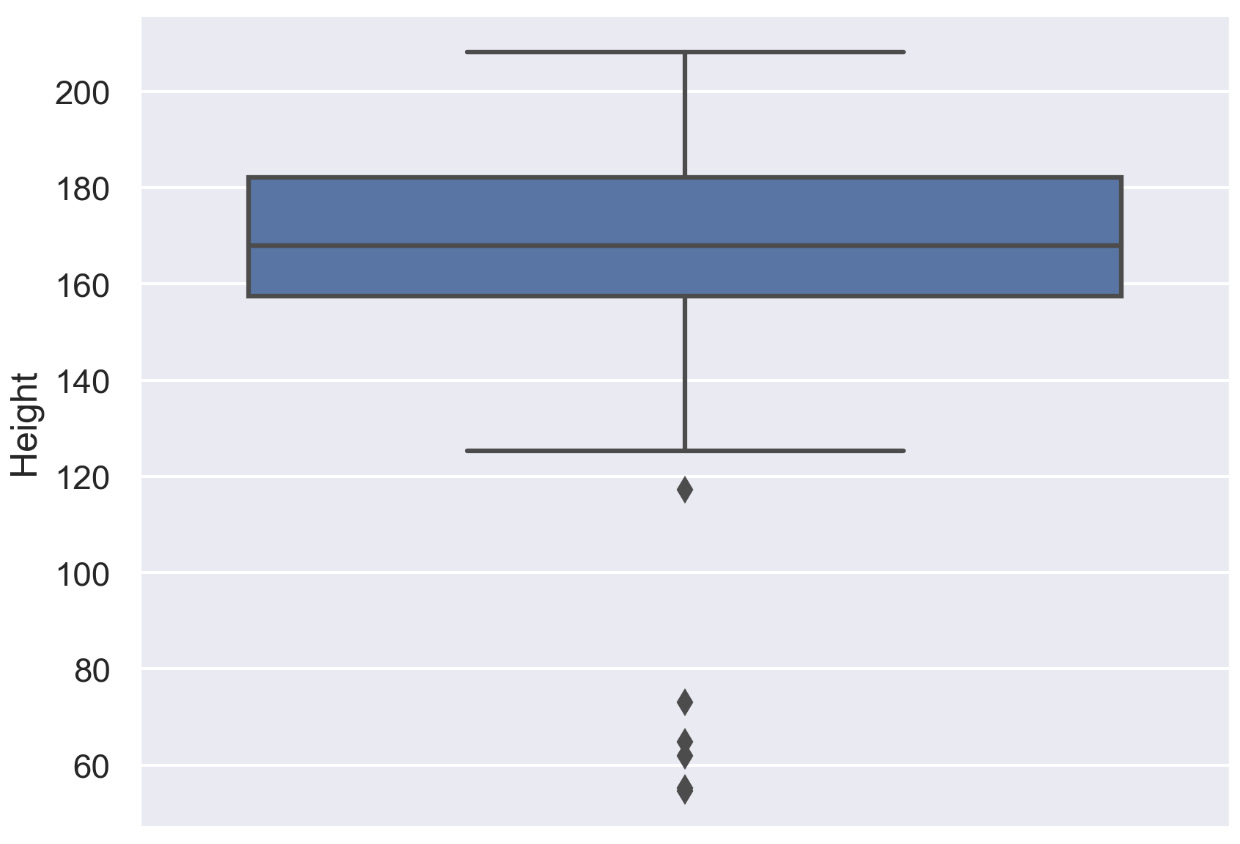
Figure 2.33: Box plot showing a single variable
The following diagram shows a basic box plot for multiple variables. In this case, it shows heights for two different groups – adults and non-adults:
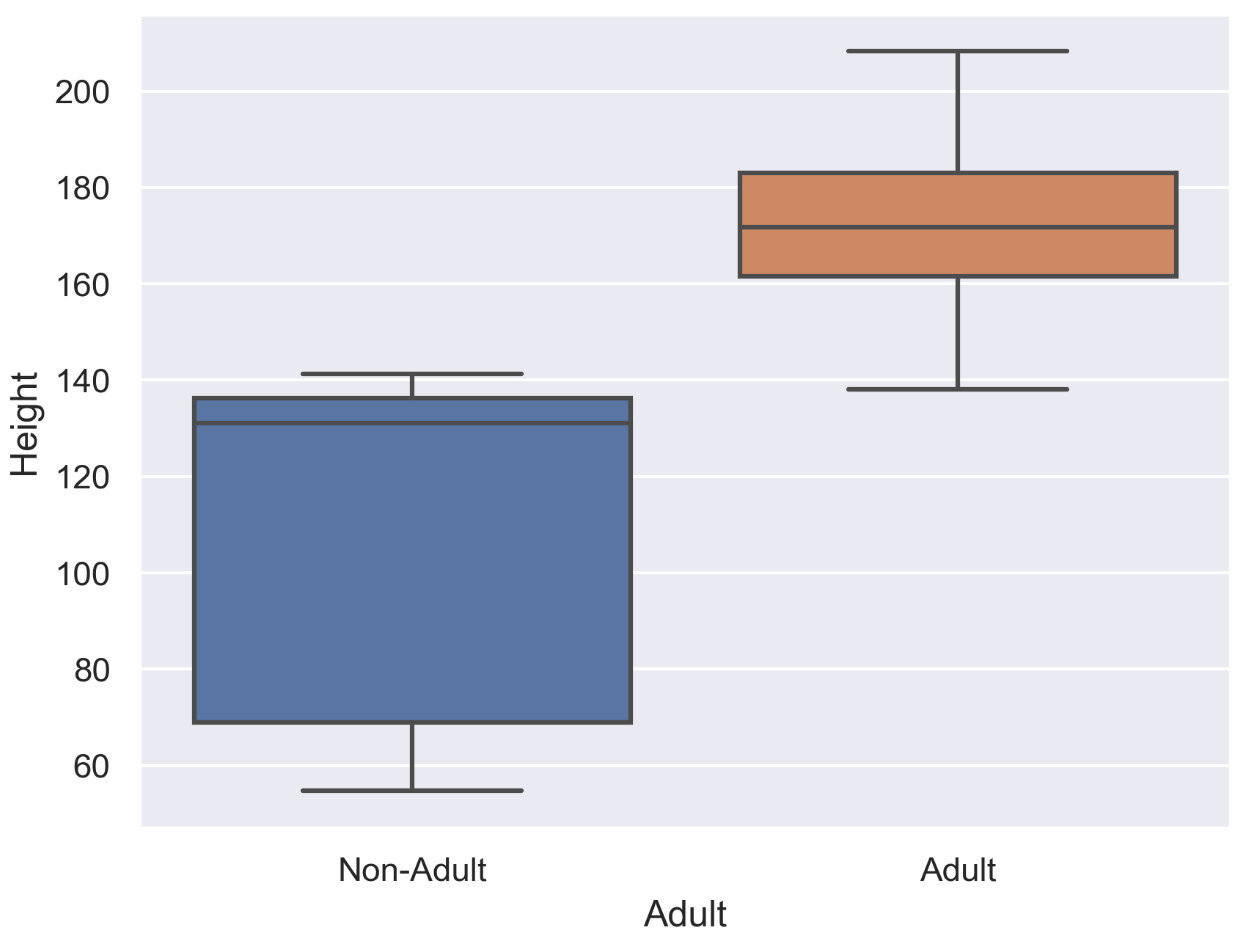
Figure 2.34: Box plot for multiple variables
In the next section, we will learn what the features, uses, and best practices are of the violin plot.
Violin Plot
Violin plots are a combination of box plots and density plots. Both the statistical measures and the distribution are visualized. The thick black bar in the center represents the interquartile range, while the thin black line corresponds to the whiskers in a box plot. The white dot indicates the median. On both sides of the centerline, the density is visualized.
Use
Compare statistical measures and density for multiple variables or groups.
Examples
The following diagram shows a violin plot for a single variable and shows how students have performed in Math:
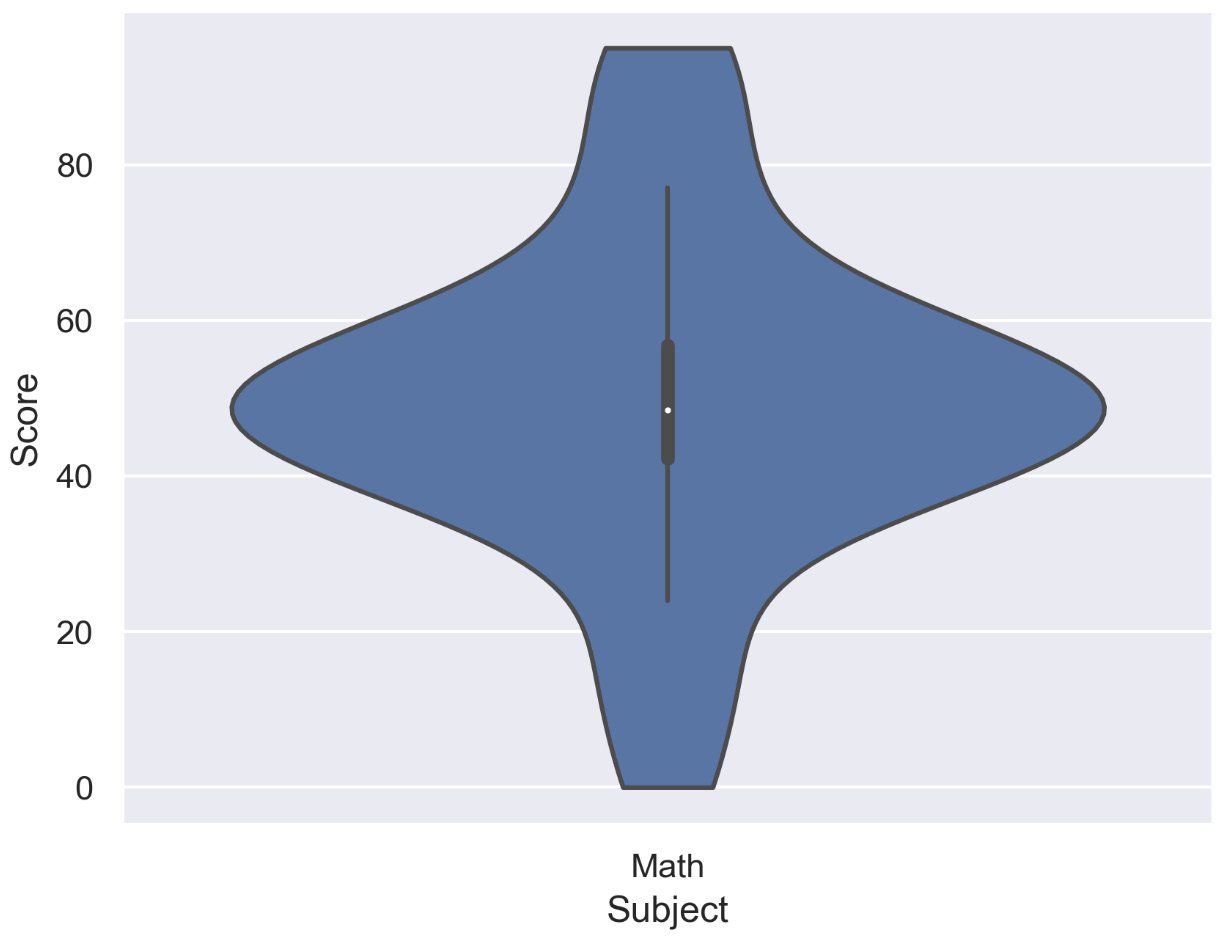
Figure 2.35: Violin plot for a single variable (Math)
From the preceding diagram, we can analyze that most of the students have scored around 40-60 in the Math test.
The following diagram shows a violin plot for two variables and shows the performance of students in English and Math:
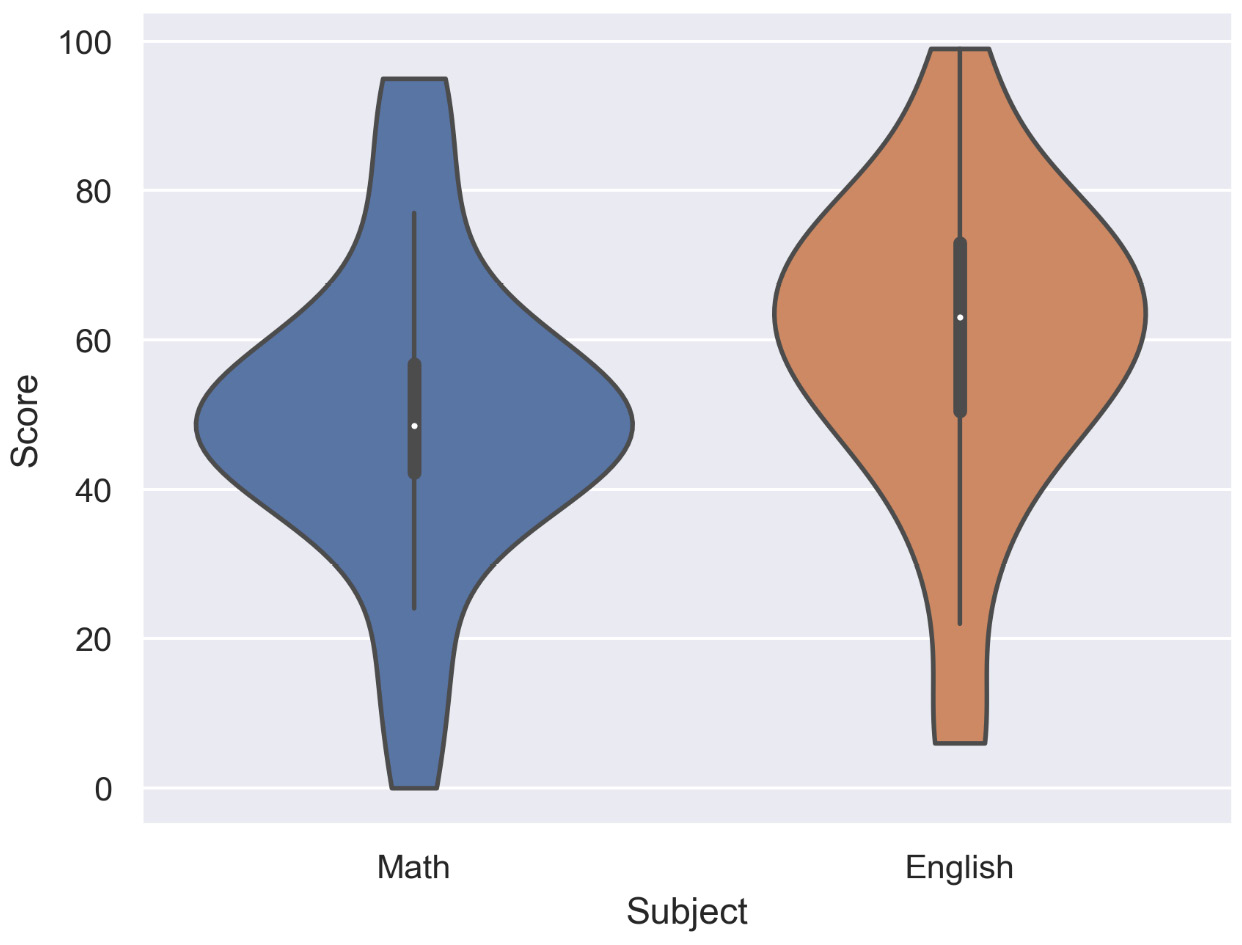
Figure 2.36: Violin plot for multiple variables (English and Math)
From the preceding diagram, we can say that on average, the students have scored more in English than in Math, but the highest score was secured in Math.
The following diagram shows a violin plot for a single variable divided into three groups, and shows the performance of three divisions of students in English based on their score:
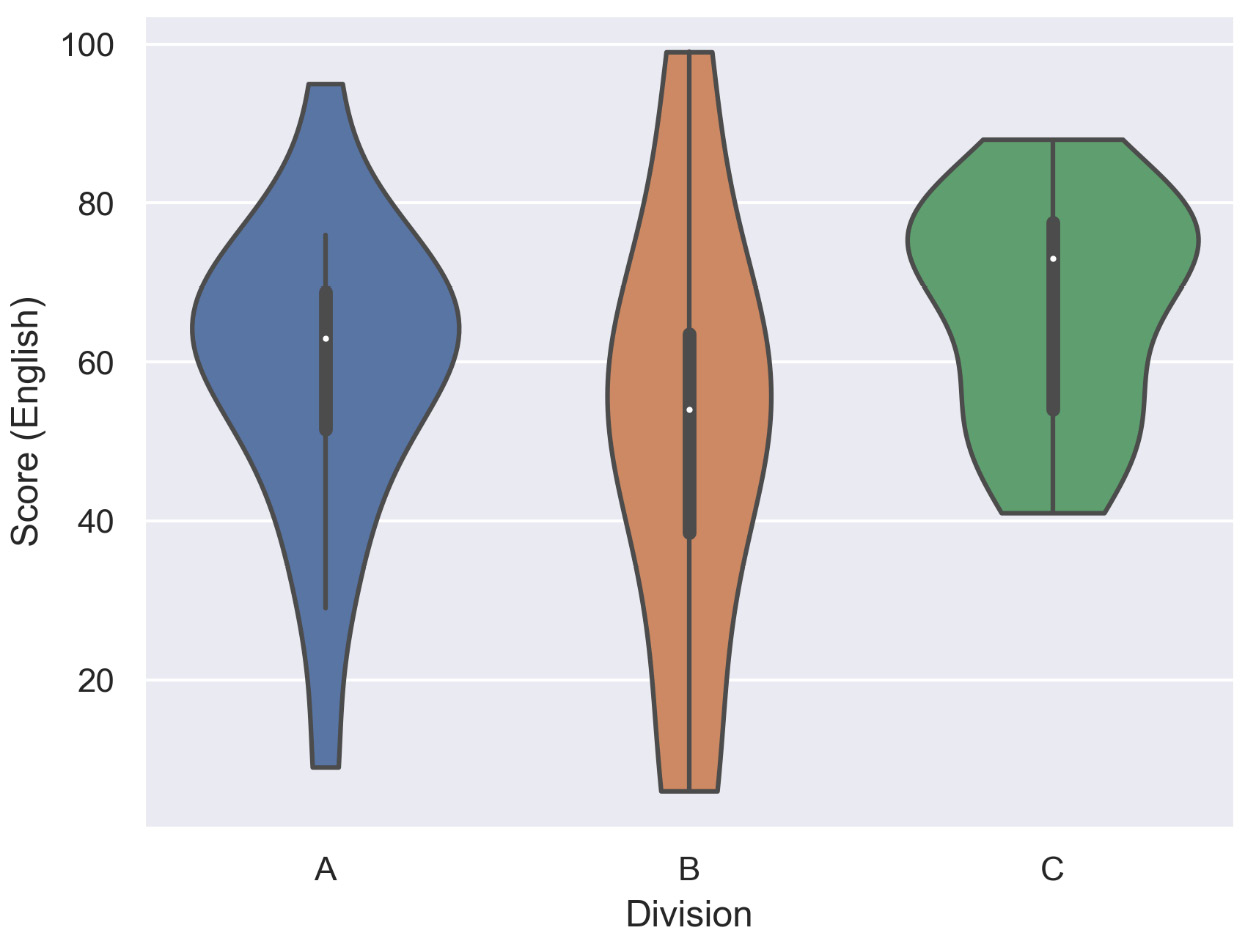
Figure 2.37: Violin plot with multiple categories (three groups of students)
From the preceding diagram, we can note that on average, division C has scored the highest, division B has scored the lowest, and division A is, on average, in between divisions B and C.
Design Practice
- Scale the axes accordingly so that the distribution is clearly visible and not flat.
In this section, distribution plots were introduced. In the following activity, we will have a closer look at histograms.
Activity 2.04: Frequency of Trains during Different Time Intervals
You are provided with a histogram that states the number of trains arriving at different time intervals in the afternoon to determine the maximum number of trains arriving in 2-hour time intervals. The goal of this activity is to gain a deeper insight into histograms:
- Looking at the following histogram, can you identify the interval during which a maximum number of trains arrive?
- How would the histogram change if in the morning, the same total number of trains arrive as in the afternoon, and if you have the same frequencies for all time intervals?
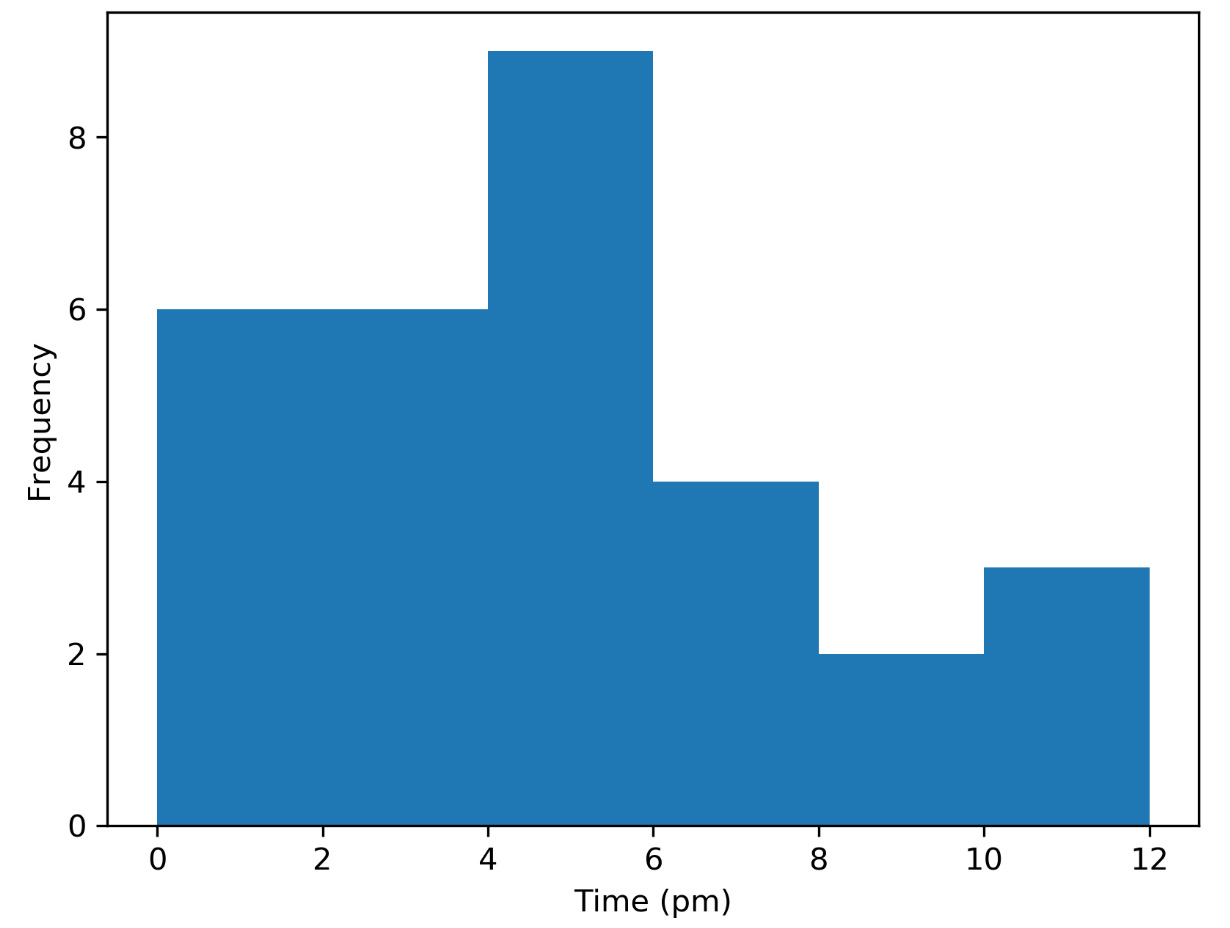
Figure 2.38: Frequency of trains during different time intervals
Note
The solution for this activity can be found via this link.
With that activity, we conclude the section about distribution plots and we will introduce geoplots in the next section.

































































