Predicting a linear congruential generator
LCGs are used in web applications to create quick and easy pseudo-random numbers. They are by nature broken and can be easily made to be predictable with enough data. The algorithm for an LCG is:
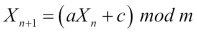
Here, X is the current value, a is a fixed multiplier, c is a fixed increment, and m is a fixed modulus. If any data is leaked, such as the multiplier, modulus, and increment in this example, it is possible to calculate the seed and thus the next values.
Getting ready
The situation here is where an application is generating random 2-digit numbers and returning them to you. You have the multiplier, modulus, and increment. This may seem strange, but this has happened in live tests.
How to do it…
Here is the code:
C = ""
A = ""
M = ""
print "Starting attempt to brute"
for i in range(1, 99999999):
a = str((A * int(str(i)+'00') + C) % 2**M)
if a[-2:] == "47":
b = str((A * int(a) + C) % 2**M)
if b[-2:] == "46":
c = str((A * int...
























































