Axis angle rotation
As discussed earlier, we can combine yaw, pitch, and roll using matrix multiplication to create a complete rotation matrix. Creating a rotation matrix by performing each rotation sequentially introduces the possibility of a Gimbal Lock.
We can avoid that Gimbal Lock if we change how a rotation is represented. Instead of using three Euler angles to represent a rotation, we can use an arbitrary axis, and some angle to rotate around that axis.
Given axis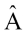 
, we can define a matrix that will rotate some angle 
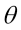around that axis:
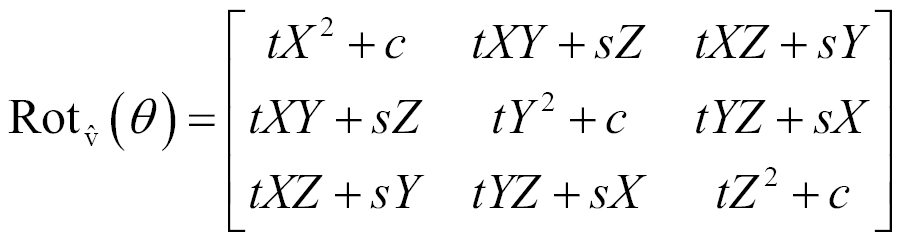
Where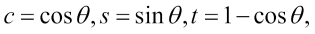 
and XYZ = Arbitrary Axis (unit length). We will explore how this matrix is derived in the How it works… section.
Getting ready
Like before, we are going to implement two versions of this function. One version will return a 4 X 4 matrix; the other will return a 3 X 3 matrix. To avoid having to constantly calculate sin and cos, we're going to create local variables for c, s, and t. The axis being passed in does not have to be normalized. Because of this...
